神经辐射场 (NeRF) – 下

NeRF：

网站： https://www.matthewtancik.com/nerf

论文：https://arxiv.org/pdf/2003.08934.pdf

代码：https://github.com/bmild/nerf

参考文献：

NeRF：用深度学习完成3D渲染任务的蹿红

【NeRF论文笔记】用于视图合成的神经辐射场技术

NeRF的数学推导

NeRF论文阅读

基本流程

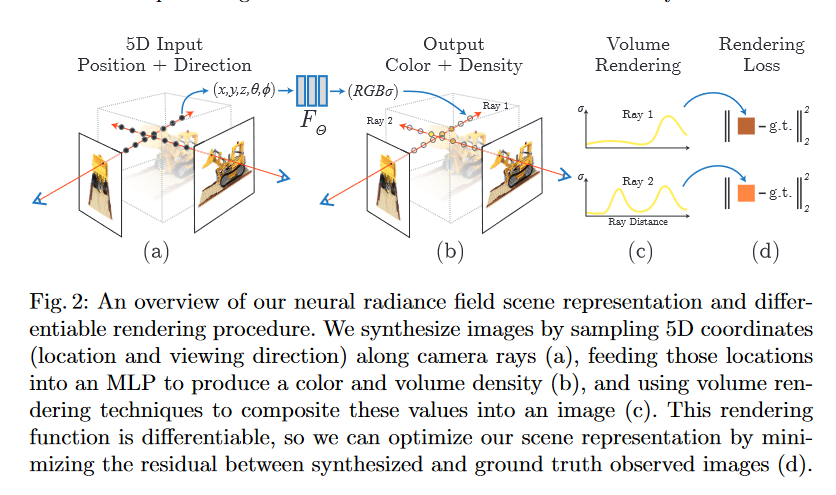
NeRF的输入是一个五维向量: （物体）空间点的位置 $\mathbf{x}=(x,y,z)$ 和（相机）观测方向 $\mathbf{d}=(\theta, \phi)$ 。输出是体密度(volume density, $\sigma$ ，可以理解为透明度)和基于观测角度的物体的空间点色彩 $\mathbf{c}=(r,g,b)$ 。

通过对每一束从相机射出的光线，计算途径空间点的色彩 $\mathbf{c}$ 和体密度 $\sigma$ 。然后基于获得的空间点的色彩和体密度，进行体素渲染（Volume Rendering）得到预测的像素值。

NeRF的网络模型（以下简称 NeRF-Model）实现的功能实际上是 $F_{\Theta}:(\mathbf{x}, \mathbf{d}) \rightarrow(\mathbf{c}, \sigma)$ 。实现了从【空间点位置 + 观测角度】到【空间点色彩+体密度】的映射。

辐射场体素渲染

辐射场体素渲染（Volume Rendering with Radiance Fields）

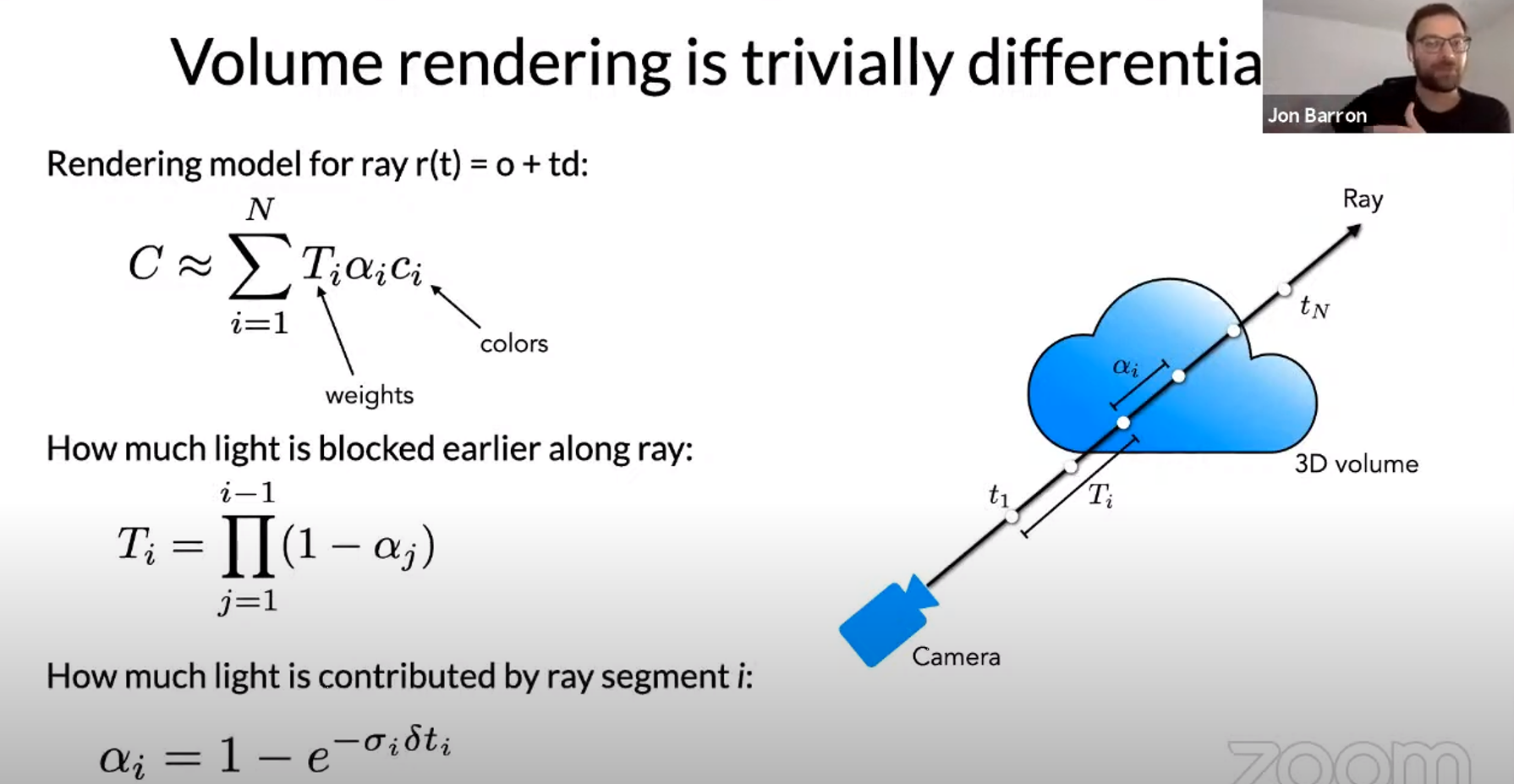
对于任意一条从相机射出的光线（ray， $\mathbf{r}$ ），我们可以通过 NeRF-Model 去预测对应路径上的所有空间点 $\mathbf{x}$ 的透明度 $\sigma(\mathbf{x})$ 和色彩 $\mathbf{c}(\mathbf{x})$ 。

这里我们假设有一条光线 $\mathbf{r}(t)=\mathbf(o)+t\mathbf(o)$ ，这条光线在空间中的范围是 $t_n$ 到 $t_f$ 。对于任意一点 $t$ , 我们可以通过 NeRF-Model 计算出它的透明度 $\sigma(t)$ 和色彩 $\mathbf{c}(t)$ 。对于这条光线上的所有点 $dt$ ，我们可以通过积分的形式，去累计他们的值，得到投射到图片上的像素值 $C(\mathbf{r})$ 。

C(\mathbf{r})=\int_{t_{n}}^{t_{f}} T(t) \sigma(\mathbf{r}(t)) \mathbf{c}(\mathbf{r}(t), \mathbf{d}) d t, \text { where } T(t)=\exp \left(-\int_{t_{n}}^{t} \sigma(\mathbf{r}(s)) d s\right)

$T(t)$ 是射线从 $t_n$ 到 $t_f$ 这一段路径上的累积透明度，可以被理解为这条射线从 $t_n$ 到 $t_f$ 一路上没有击中任何粒子的概率。

推导如下：

假设 $T^*(t)=\sigma(t)dt$ 定义为为在 $t$ 点击中粒子的概率（瞬时透明度）。则在 $t$ 没有点击中粒子的概率为 $1-T^*(t)=1-\sigma(t)dt$ 。
因此，在 $t+dt$ 点前没有没有被击中的概率 $T(t+dt)$ 为, $T(t)$ (一路上没有击中任何粒子的概率) 和 $1-\sigma(t)dt$ (在 $t$ 没有点击中粒子) 的乘积：

\begin{align*} T(t+dt) &= T(t) \times (1-\sigma(t)dt)\\ T(t)+T'(t)dt &=T(t)-T(t)\sigma(t)dt\\ \frac{T^{\prime}(t)}{T(t)} dt &=-\sigma(t) d t\\ log(T(t)) &=-\int_{t_{0}}^{t} \sigma(s) d s\\ T(t)&=exp(-\int_{t_{0}}^{t} \sigma(s) d s)\\ \end{align*}

离散化的表示形式：

优化神经辐射场

概述：在训练阶段，输入一系列（如100张）图片和他们的拍摄相机角度、内参、场景边界（可以使用COLMAP获得）。然后优化NeRF网络（几层MLP）。训练过的NeRF，可以实现任意角度的渲染。

两个提升

两项设计帮助提升高分辨率复杂场景的性能

1. 位置编码

[35] Rahaman, N., Baratin, A., Arpit, D., Dr ̈ axler, F., Lin, M., Hamprecht, F.A., Bengio, Y., Courville, A.C.: On the spectral bias of neural networks. In: ICML (2018)

神经网络倾向于学习低频函数 [35]。输入网络之前，把输入信号映射到高维空间可以帮助网络更好的适应高频变化。这个观点在 Transformer 的文章中多次被使用，即位置编码(Positional encoding)。具体做法如下：

对于输入的三个位置坐标 $\mathbf{x}=(x,y,z)$ 和观测角度 $\mathbf{d}=(\theta, \phi)$ , 他们的取值范围归一化到 [-1, 1]。对于每一个数值，例如 $p\in\mathbb{R^1}$ , 通过函数 $\gamma(\cdot)$ 映射到 $\mathbb{R^{2L}}$ 空间中，这里 $L$ 指的是编码的数量，对于位置坐标， $L=10$ ；对于观测角度， $L=4$ 。

\gamma(p)=\left(\sin \left(2^{0} \pi p\right), \cos \left(2^{0} \pi p\right), \cdots, \sin \left(2^{L-1} \pi p\right), \cos \left(2^{L-1} \pi p\right)\right)

对比Transformer中的 positional encoder，Transformer主要是用它为Token提供离散的位置编码没有位置顺序的概念。而我们的位置编码，使用连续的空间位置作为输入，映射到了一个连续的高维空间。从而帮助后面的MLP网络封号的学习高频信息。

效果对比：
Complete Model V.S. No Position Encoding

2. 分层取样

分层取样（Hierarchical volume sampling）：渲染的速度是一个关键的因素。空白的空间和遮盖的空间对于最终渲染出来的像素没有帮助，因而可以省略。

NeRF使用了两个网络进行优化：粗糙（coarse）和调整（fine）。首先，在一条光线上，使用分层抽样（stratified sampling）抽样 $N_c$ 个点，使用coarse网络推理，重写之前的体素渲染公式：

分层随机抽样：一般地，按一个或多个变量把总体划分成若干个子总体，每个个体属于且仅属于一个子总体，在每个子总体中独立地进行简单随机抽样，再把所有子总体中抽取的样本合在一起作为总样本，这样的抽样方法称为分层随机抽样，每一个子总体称为层。
摘自: https://zhuanlan.zhihu.com/p/478685602

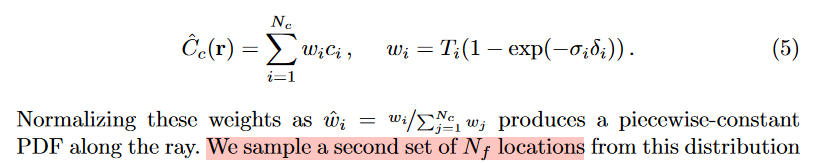
这里权重是归一化的概率分布密度（PDF）。我们再使用逆变换采样（inverse transform sampling）抽取 $N_f$ 个点，放入fine网络进行推理。这样总共可以得到 $N_c+N_f$ 个点。然后再使用前面体素渲染的公式对这 $N_c+N_f$ 个点进行计算，得到最终的像素值。

逆变换采样:如何通过均匀分布来采样服从目标函数（体素密度分布）分布的样本集。
https://blog.csdn.net/anshuai_aw1/article/details/84840446

具体实现

在每次优化迭代中，随机从数据集中选取一组从相机射出的光线（ray），然后采样 $N_c$ 和 $N_c+N_f$ 个样本分别训练coarse和fine网络。基于体素渲染的方法，得到像素值和ground truth 对比计算 MSE loss。进而训练神经网络。

具体的，batch size 是4096个光线， $N_c=64$ ， $N_f=128$ 。优化器是Adam（ $\beta_1=0.9$ , $\beta_2=0.999$ , $\epsilon=10^{-7}$ ）, 学习率 $5 \times 10^{-4}$ 等。整个训练需要100-300k 次迭代（细节请参照论文）。