神经辐射场 (NeRF) – 上
- 网站: https://www.matthewtancik.com/nerf
- 论文:https://arxiv.org/pdf/2003.08934.pdf
- 代码:https://github.com/bmild/nerf
参考文献:
体素渲染
体素渲染 (Volume Rendering)
[2] Kajiya J T, Von Herzen B P. Ray tracing volume densities[J]. ACM SIGGRAPH computer graphics, 1984, 18(3): 165-174.
论文中首先介绍了经典的体素渲染(volume rendering) [2] 方法。体素密度 \sigma(\mathbf{x}) 可以被理解为,一条射线 \mathbf{r} 在经过 x 处的一个无穷小的粒子时被终止的概率,这个概率是可微的。换句话说,有点类似于这个点的不透明度。由于一条射线上的点是连续的,自然的想法是这条射线的颜色可以由积分的方式得到。将一个相机射线标记为 \mathbf{r}(t)=\mathbf{o}+t\mathbf{d} ,这里 \mathbf{o} 是射线原点, \mathbf{d} 是前述的相机射线角度,t 的近段和远端边界分别为 t_n 以及 t_f 。T(t) 是射线从 t_n 到 t_f 这一段路径上的累积透明度,可以被理解为这条射线从 t_n 到 t_f 一路上没有击中任何粒子的概率。
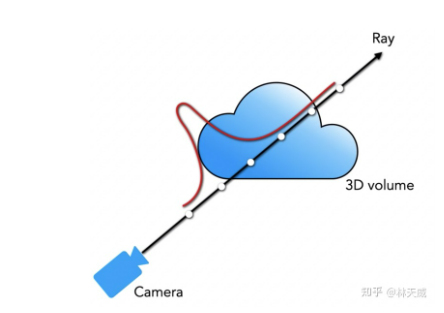
那么这条射线的颜色,则可以用积分的方式表示为:
C(r)=\int_{t_{n}}^{t_{f}} T(t) \cdot \sigma(\boldsymbol{r}(t)) \cdot \boldsymbol{c}(\boldsymbol{r}(t), \boldsymbol{d}) d t
假设T^*(t)=\sigma(t)dt 定义为为在 t 点击中粒子的概率(瞬时透明度)。则在t 没有点击中粒子的概率为 1-T^*(t)=1-\sigma(t)dt
因此,在 t+dt 点前没有没有被击中的概率 T(t+dt) 为, T(t) (一路上没有击中任何粒子的概率) 和 1-\sigma(t)dt (在t 没有点击中粒子) 的乘积:
\begin{align*} T(t+dt) &= T(t) \times (1-\sigma(t)dt)\\ T(t)+T'(t)dt &=T(t)-T(t)\sigma(t)dt\\ \frac{T^{\prime}(t)}{T(t)} dt &=-\sigma(t) d t\\ log(T(t)) &=-\int_{t_{0}}^{t} \sigma(s) d s\\ T(t)&=exp(-\int_{t_{0}}^{t} \sigma(s) d s)\\ \end{align*}我们使用离散化的函数取代色彩和透明度函数:
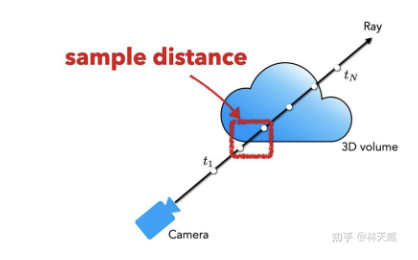
\hat{C}(\boldsymbol{r})=\sum_{i=1}^{N} T_{i} \cdot\left(1-\exp \left(-\sigma_{i} \cdot \delta_{i}\right)\right) \cdot \boldsymbol{c}_{i}
这里是邻近两个采样点之间的距离 \delta_{i}=t_{i+1}-t_{i},此处 T(t):
辐射场
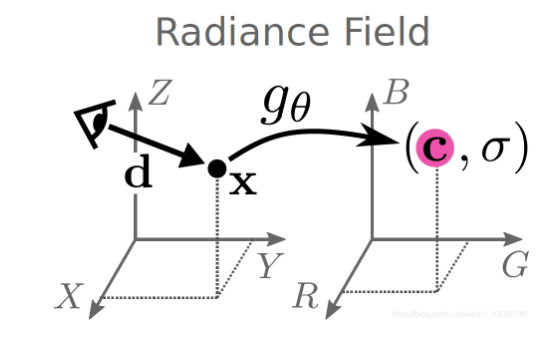
辐射场(Radiance Fields, RF)是指一个函数、或者说映射 g_{\theta}。如上图所示,人(相机)在位置 \mathbf{d}\in \mathbb{S}^{2}观测世界坐标系 XYZ 中的点 \mathbf{x} \in \mathbb{R}^{3},通过一个隐式的函数 g_{\theta}, 得到 RGB 色彩空间的值\mathbf{c} \in \mathbb{R}^{3}及一个\sigma \in \mathbb{R}^{+}是volume density(可以简单理解为透明度)。:
(\sigma, \mathbf{c})=g_{\theta}(\mathbf{x}, \mathbf{d})对于这个函数:
- 输入是:\mathbf{x} \in \mathbb{R}^{3} 是三维空间点的坐标;\mathbf{d}\in \mathbb{S}^{2}是观察角度。
- 输出是:\sigma \in \mathbb{R}^{+}是volume density(可以简单理解为透明度);\mathbf{c} \in \mathbb{R}^{3}是三通道颜色(color)。
辐射场 (RF) 是对三维场景的隐式表达(implicit scene representation)。Neural Radiance Fields(NeRF)则是指用神经网络拟合Radiance Fields这个函数。该神经网络具体是多层感知机。