对极几何(Epipolar Geometry)
参考文献:
目的
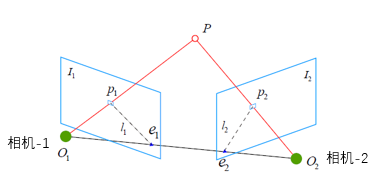
我们希望求取两帧图像I_1和 I_2 之间的运动,设第一帧到第二帧的运动为R; t。两个相机中心分别为O_1;O_2。现在,考虑I1 中有一个特征点p_1,它在I_2 中对应着特征点p_2。我们晓得图像上这两个点对应的是空间中的同一个点P。即 p_{1}=K P, \quad p_{2}=K(R P+t)。K 为相机内参矩阵.
本质矩阵(Essential matrix)
我们知道由相机1到相机2是刚体运动,那么观测点P在相机1坐标系的坐标就可以通过刚体转换变成相机2坐标系下,
这里的 x_1 和 x_2 是两个像素点的归一化平面上的坐标: x_{1}=K^{-1} p_{1}, \quad x_{2}=K^{-1} p_{2}。
x_2=R x_1 +T
其中R和T分别表示旋转和平移,如果我们将其左叉乘一个T,即:
\begin{align*} T\times x_2&=T\times \left( Rx_1+T \right) \\ &=T\times Rx_1+T\times T \\ &=T\times Rx_1 \end{align*}其中 T\times x_2 表示对极平面的法线,若再左点乘一个x_2^T得到以下公式。
- 因为x_2与法线 T\times x_2垂直,所以左侧为0。
- 我们知道两向量的叉乘可以转换为一向量的反对称矩阵与另一向量的点乘,其中[T_\times]表示T的反对称矩阵.
- 令E=[T_\times] R
-
本质矩阵E 定义:
x_2^TEx_1=0 -
基本矩阵 定义: F=K^{-T} E K^{-1},带入上式可以得到:
p_2^TFp_1=0
本质矩阵 E 和基本矩阵F 只相差了相机内参K。
本质矩阵的性质:
- E 乘以任意非零常数后,对极约束依然满足。我们把这件事情称为E 在不同尺度下是等价的。
- 根据E=[T_\times] R,可以证明[3],本质矩阵E 的奇异值必定是[\delta; \delta; 0]^T 的形式
- 由于平移和旋转各有三个自由度,故[T_\times] R共有六个自由度。但由于尺度等价性,故E 实际上有五个自由度
相机位姿估计
相机位姿估计问题变为以下两步:
- 根据配对点的像素位置,求出 E 或者 F;
- 根据 E 或者 F,求出 R 和 t。
E 具有五个自由度的事实,表明我们最少可以用五对点来求解E。但是,E 的内在性质是一种非线性性质,在求解线性方程时会带来麻烦,因此,也可以只考虑它的尺度等价性,使用八对点来估计E——这就是经典的八点法(Eight-point-algorithm)。
考虑一对匹配点,它们的归一化坐标为:x1 = [u1; v1; 1]^T , x2 = [u2; v2; 1]^T 。根据对极约束,有
\left(u_{1}, v_{1}, 1\right)\left(\begin{array}{lll} e_{1} & e_{2} & e_{3} \\ e_{4} & e_{5} & e_{6} \\ e_{7} & e_{8} & e_{9} \end{array}\right)\left(\begin{array}{c} u_{2} \\ v_{2} \\ 1 \end{array}\right)=0令 e=\left[e_{1}, e_{2}, e_{3}, e_{4}, e_{5}, e_{6}, e_{7}, e_{8}, e_{9}\right]^{T},可得:
\left[u_{1} u_{2}, u_{1} v_{2}, u_{1}, v_{1} u_{2}, v_{1} v_{2}, v_{1}, u_{2}, v_{2}, 1\right] \cdot e=0
如果我们有8个对应的点 (u_{1}^{1}, v_{1}^{1}, u_{2}^{1}, v_{2}^{1})~(u_{1}^{8}, v_{1}^{8}, u_{2}^{8}, v_{2}^{8}),可得:
\left(\begin{array}{ccccccccc}
u_{1}^{1} u_{2}^{1} & u_{1}^{1} v_{2}^{1} & u_{1}^{1} & v_{1}^{1} u_{2}^{1} & v_{1}^{1} v_{2}^{1} & v_{1}^{1} & u_{2}^{1} & v_{2}^{1} & 1 \\
u_{1}^{2} u_{2}^{2} & u_{1}^{2} v_{2}^{2} & u_{1}^{2} & v_{1}^{2} u_{2}^{2} & v_{1}^{2} v_{2}^{2} & v_{1}^{2} & u_{2}^{2} & v_{2}^{2} & 1 \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \\
u_{1}^{8} u_{2}^{8} & u_{1}^{8} v_{2}^{8} & u_{1}^{8} & v_{1}^{8} u_{2}^{8} & v_{1}^{8} v_{2}^{8} & v_{1}^{8} & u_{2}^{8} & v_{2}^{8} & 1
\end{array}\right)\left(\begin{array}{l}
e_{1} \\
e_{2} \\
e_{3} \\
e_{4} \\
e_{5} \\
e_{6} \\
e_{7} \\
e_{8} \\
e_{9}
\end{array}\right)=0
它的系数矩阵由特征点位置构成,大小为8\times9。e 位于该矩阵的零空间中。如果系数矩阵是满秩的(即秩为8),那么它的零空间维数为1,也就是e 构成一条线。这与e 的尺度等价性是一致的。
接下来对E进行SVD分解即可得到R和t。假设对E的分解结果为:
\boldsymbol{E}=\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{T}其中U 和 V为正交阵,\Sigma 为奇异值矩阵。根据E的内在性质,我们知道 E= diag[\delta; \delta; 0]^T。
在SVD 分解中,对于任意一个E,存在两个可能的 t、R 与它对应:
其中\boldsymbol{R}_{Z}\left(\frac{\pi}{2}\right) 表示沿 Z 轴旋转 90 度得到的旋转矩阵。同时,由于 -E 和 E 等价,所以对任意一个t 取负号,也会得到同样的结果。因此,从E 分解到t;R 时,一共存在四个可能的解。
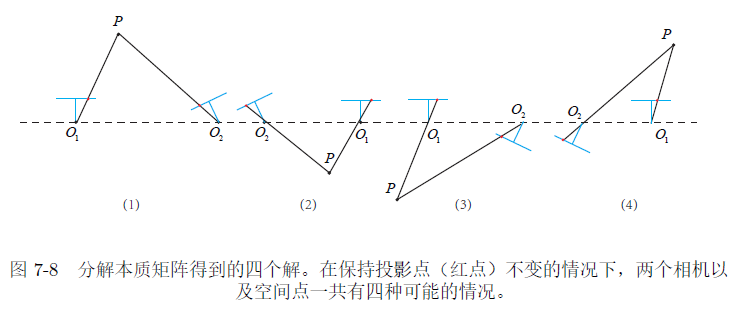
幸运的是,只有第一种解中,P 在两个相机中都具有正的深度。因此,只要把任意一点代入四种解中,检测该点在两个相机下的深度,就可以确定哪个解是正确的了。
剩下的问题还有一个:根据线性方程解出的E,可能不满足E 的内在性质——它的奇异值不一定为E= diag[\delta; \delta; 0]的形式。
通常的做法做法是将奇异值矩阵取成 diag(1; 1; 0),因为E 具有尺度等价性,这样做也是合理的。
得到t、R后,我们可以实现从相机1到相机2的变换。
x_2 = Rx_1 + t