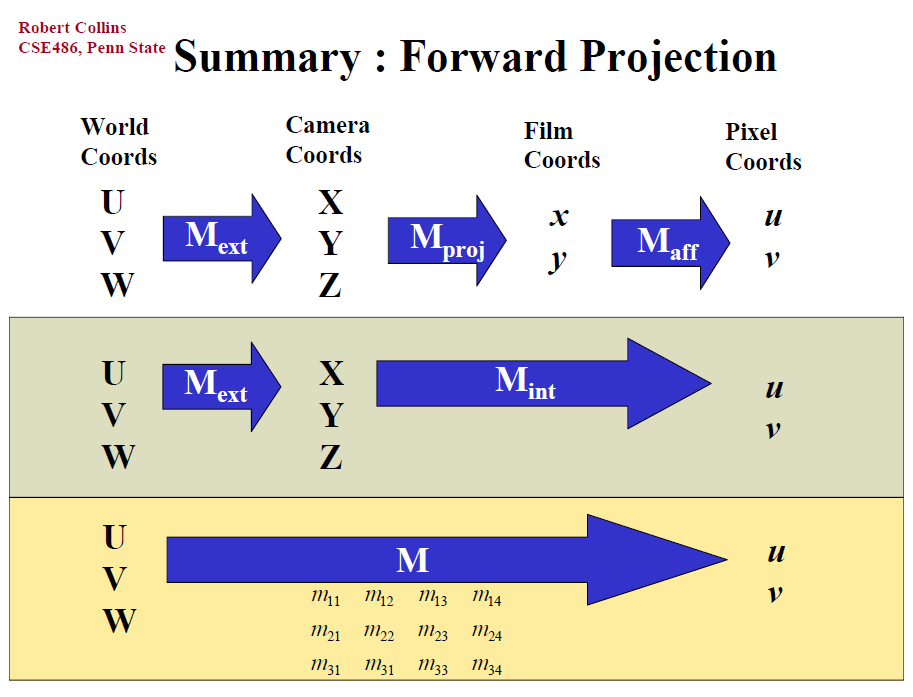
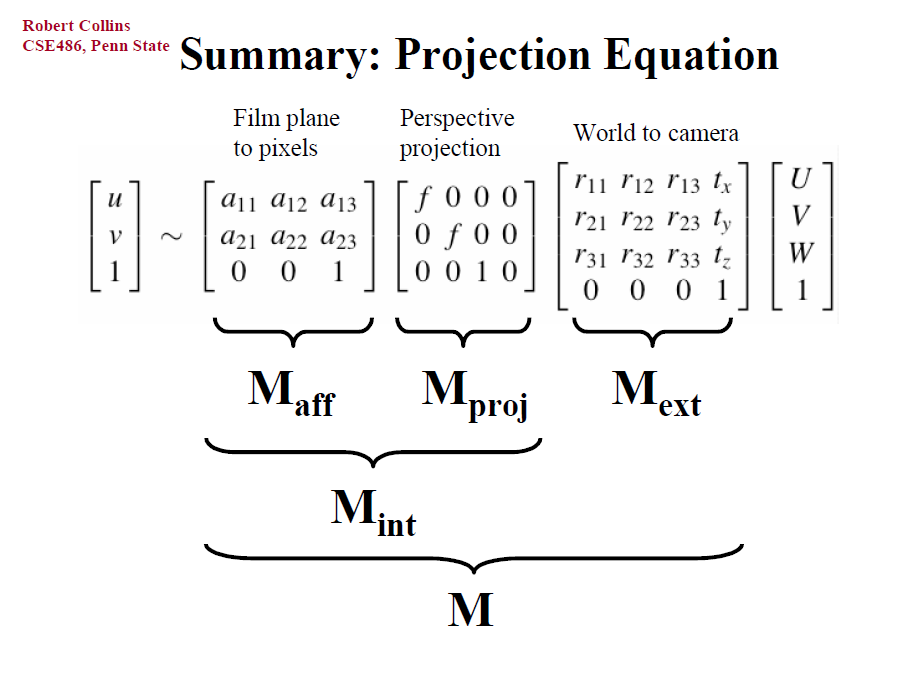
成像模型 (Camera_Projection)

参考自课件：

• (Camera Projection – 1)[https://www.cse.psu.edu/~rtc12/CSE486/lecture12.pdf]
• (Camera Projection – 2)[https://www.cse.psu.edu/~rtc12/CSE486/lecture13.pdf]
• https://mp.weixin.qq.com/s/qxLgnWELQ2ZI4MyreXGOYQ

我们需要一个数学模型来描述如何将 3D 世界坐标系中的点 (U,V,W) 投影到 2D 图片坐标系 ($u$,$v$) 中。

Camera Coords to Film Coords (3D to 2D)

相机坐标系 Camera Coords ($X$,$Y$,$Z$) to 画布坐标系 Film Coords ($x$,$y$):

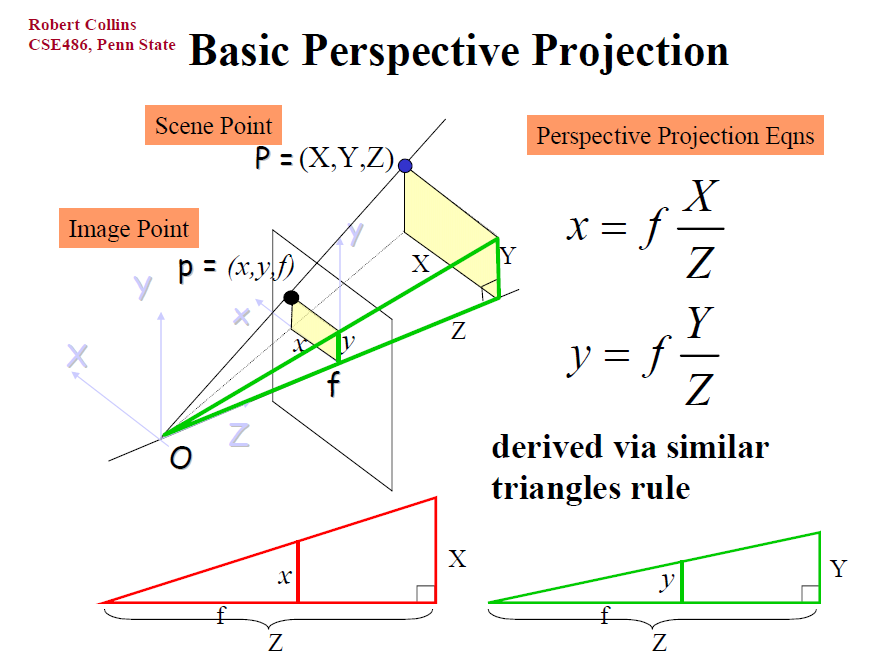
对于相机坐标系中的点（$X$,$Y$,$Z$），其中$Z$ 是从相机原点到该点的距离。已知焦距$f$, 因此，相机坐标系到画布坐标系的比例关系为 $f/Z$。

对应的，我们想求此点在画布坐标系中的横纵坐标（$x,y$），只需要按比例缩放：

因此， 变换方程可以写作
$$\left[\begin{array}{c} x\\ y \\ z \end{array}\right]=\left[\begin{array}{llll} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}\right]\left[\begin{array}{c} X \\ Y \\ Z \\ 1 \end{array}\right]$$
其中$z$ 为虚构的第三维坐标， Camera Coords ($X$,$Y$,$Z$,1) 中的 1 为预留的位置偏移量。

World Coords to Camera Coords (3D to 3D)

世界坐标系 World Coords ($\mathbf{P}_{\mathrm{W}}$) 到相机坐标系 Camera Coords ($\mathbf{P}_{\mathrm{C}}$) 只需要简单的旋转$\mathbf{R}$ 和偏移$\mathbf{C}$.

因此，变换方程可以写作

$$\begin{gathered} \mathbf{P}_{\mathbf{C}}=\mathbf{R}\left(\mathbf{P}_{\mathbf{W}}-\mathbf{C}\right) \\ \left(\begin{array}{l} \mathrm{X} \\ \mathrm{Y} \\ \mathrm{Z} \\ 1 \end{array}\right)=\left(\begin{array}{llll} \mathrm{r}_{11} & \mathrm{r}_{12} & \mathrm{r}_{13} & 0 \\ \mathrm{r}_{21} & \mathrm{r}_{22} & \mathrm{r}_{23} & 0 \\ \mathrm{r}_{31} & \mathrm{r}_{32} & \mathrm{r}_{33} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)\left(\begin{array}{llll} 1 & 0 & 0 & -c_{x} \\ 0 & 1 & 0 & -c_{y} \\ 0 & 0 & 1 & -c_{z} \\ 0 & 0 & 0 & 1 \end{array}\right)\left(\begin{array}{c} \mathrm{U} \\ \mathrm{V} \\ \mathrm{W} \\ 1 \end{array}\right) \end{gathered}$$
其中 偏移$\mathbf{C}=(c_{x},c_{y},c_{z})$。

偏移的例子：两个相机，一个在（0，0，0），另一个在（$\mathbf{T}_x$，0，0）, 对于点（X,Y,Z）的观测

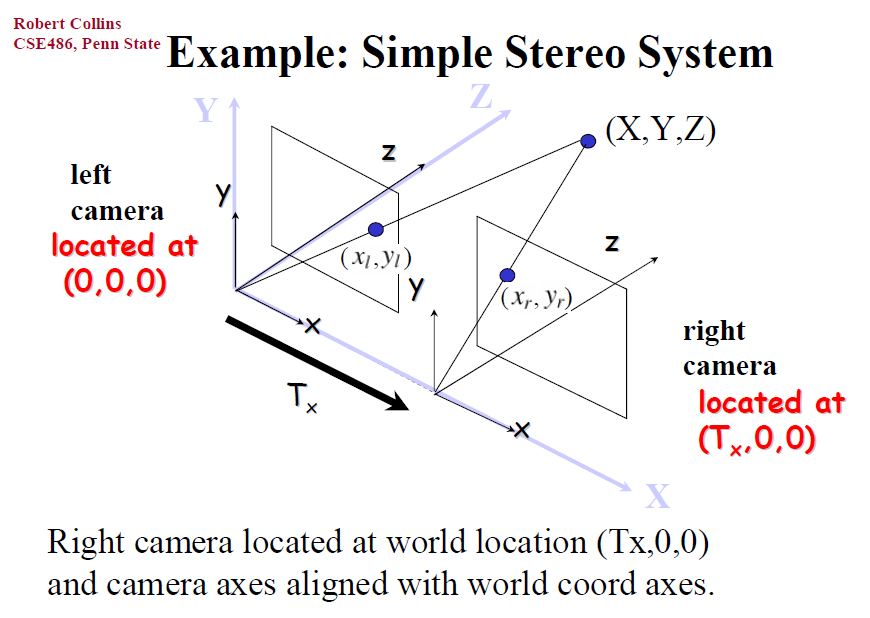
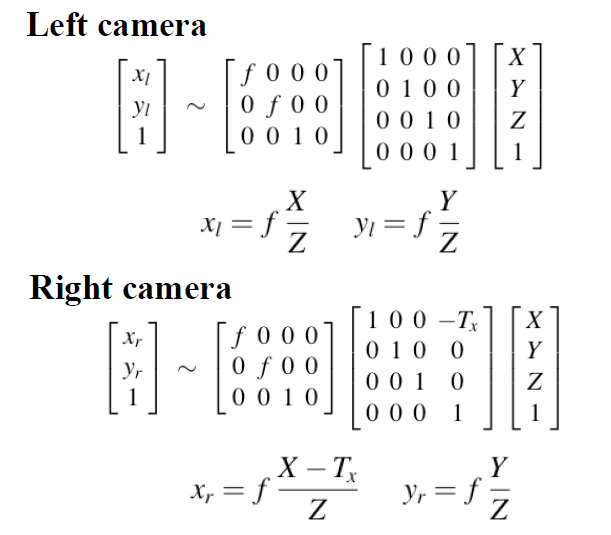
通常写法

Film Coords to Pixel Coords (2D to 2D)

画布坐标系 到 像素坐标系： 仿射变换 Affine Transformation

主要有两个方面

• 偏移量 offset: $o$
• 尺度变换 scales： $s$

$$u=\frac{1}{\mathrm{~s}_{\mathrm{x}}} f\cdot x+o_{x} =\frac{1}{\mathrm{~s}_{\mathrm{x}}} f \frac{X}{Z}+o_{x} \\$$
$$v=\frac{1}{\mathrm{~s}_{\mathrm{y}}} f\cdot y+o_{y}=\frac{1}{\mathrm{~s}_{\mathrm{y}}} f \frac{Y}{Z}+o_{y}$$
注意，方向 可能会变化，此时，需要考虑增加正负号。

总结